性能的衡量
对于聚类,当我们评判聚类的效果好坏时,我们通常是希望
- 类间越分开越好;
- 类内越紧凑越好
这种情况下,就需要定义各种类内的距离和类间的距离了。这里,我们不作为重点讲,有兴趣的同学可以看看周克华老师的«机器学习»这本书,里面讲的挺详细。
下面我们分别来讲讲在聚类中常用的几种算法。
K-means
Talk is cheap, show you the code.
输入: 数据集: ,簇的数目:
输出: 簇:
k-means(){
for i=1,2,...k
随机选择数据样本为簇k的初始中心
end
while(簇中心不再变化)
for i=1,2,...,n
for j=1,2,...,k
计算样本i到簇中心j的距离
end
给样本赋予最近的簇中心的编号
end
for i=1,2,...,k
更新簇中心为簇中所有样本的均值
end
end while
}
从上面的伪码中可以发现,K-means中有几处是随机或者需要认为设定的:
- k的取值,也就是簇的数目,这个需要认为设定
- 初始化簇中心
- 距离的定义
正是以上三者,对K-means算法的影响很大。
k如何选取
如何选取最优的k呢?显然,当我们说某个东西“最优”时,我们需要一个性能指标去衡量。在这里,通常我会定义聚类的异构性函数:
其中,是总的样本数;是簇的数目;是簇的聚类中心。
选取合适的k的时候,我们就是看异构性函数在k的变化下是如何变化的。
对于,k的取值,我们先看一张图。 可以看到,毫无疑问,随着k的增加,异构性函数越来越小,可以想象,当簇数k=样本数n时,异构性函数为0。
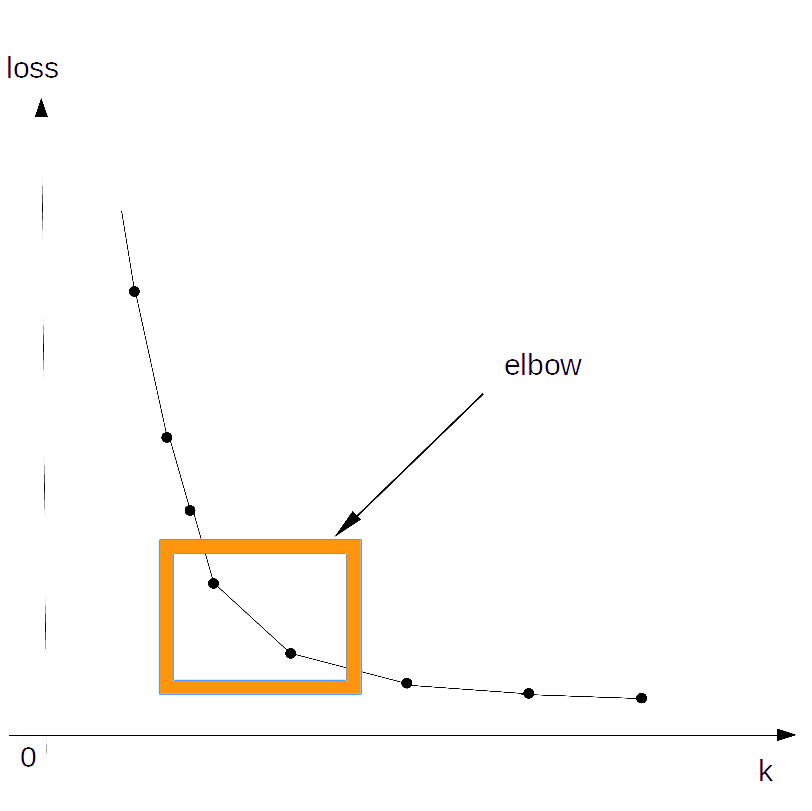
在k很小的时候,随着k的增大,异构性函数急剧降低;然后会经历一个平滑的过度期(我们称之为elbow);在之后减少的速度非常慢。
我们会选择elbow中的某个k,也就是k的增大对l的减少有很大收益的k
如何初始化簇中心
另外,当确定k后,簇中心的初始化也是非常重要的。不然很容易陷入局部最优,例如下面这两个由于不同的初始化而产生的簇:
对于初始化,有一种方法,称之为smart initialization,相应的k-means被称之为k-means++。
从数据样本中随机选择一个数据点作为第一个簇的中心
while 样本中心未选够k个
对于每一个样本,计算其最近的簇中心的距离
从数据样本中选择新的簇中心,选择的概率与样本到簇中心的距离的平方成正比
end while
上面这个算法,应该是比较容易理解,目的就是要使簇中心分开的尽量远。
实验证明采用smart initialization和普通的初始化相比有以下优点和缺点。
Pros:
- 可以改善簇的分布陷入局部最优的情况
- 后续的k-means收敛更快
Cons:
- 前期初始化计算量比原始的大很多
距离的定义
关于这一点,我想无需多言,针对具体的应用,不同的距离度量有不同的效果,最常见的就是欧式距离了。
k-means的局限性
在k-means中,我们采用的是hard assignment。也就是说,每个数据样本只能属于某一个簇。但有时侯,比如说,当我们对新闻聚类时,对于某个新闻,假设它百分之60的内容是涉及政治,百分之40的内容是涉及体育,对于这种不确定性,只是简单的将新闻聚类到某一簇中是不太合适的。
另外,可以发现K-means自带的属性就是簇的形状是圆形的,即使可以对坐标进行加权处理,产生的也都是和坐标轴对齐的椭圆。

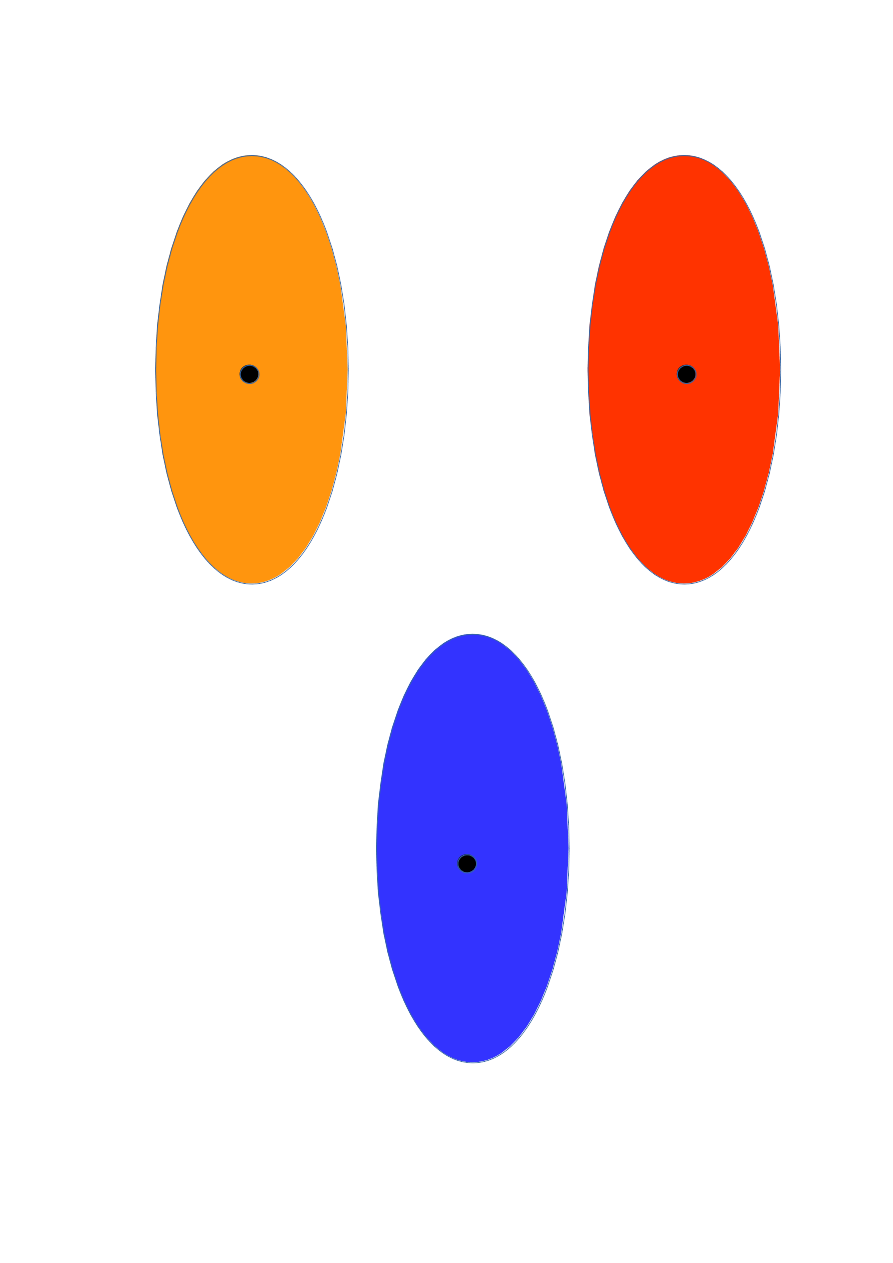
但是我们可以看一些K-means失效的情况。比如下面几个例子:
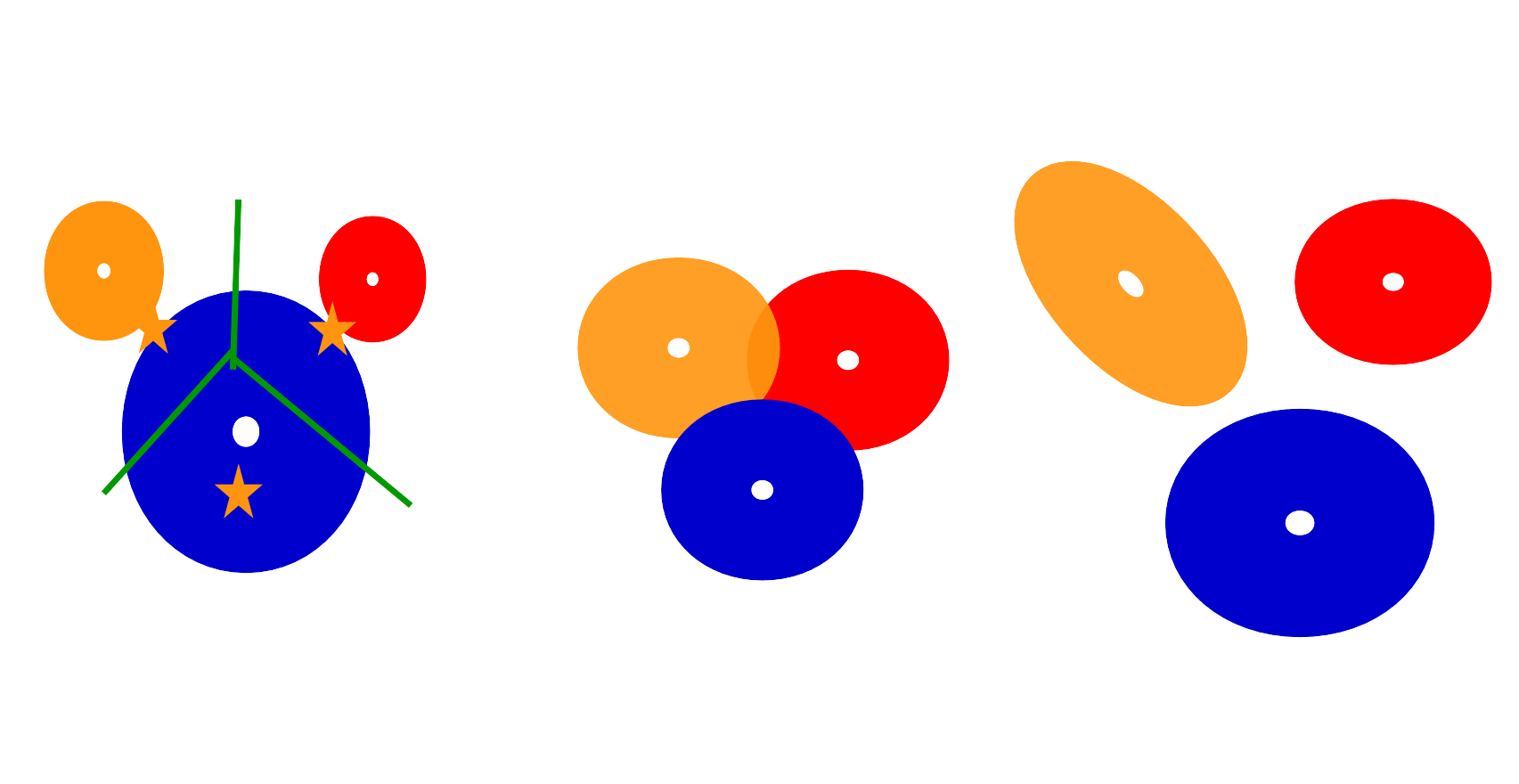
第一个例子,由于簇的大小不一样,导致簇中心的偏移;第二个例子,簇中样本的重叠这种情况k-means无法处理;第三个例子,簇的方向并为与坐标轴对齐,这种k-means也无法处理。
参考文献
[1] 机器学习,周克华