k-means的局限性
在k-means中,我们采用的是hard assignment。也就是说,每个数据样本只能属于某一个簇。但有时侯,比如说,当我们对新闻聚类时,对于某个新闻,假设它百分之60的内容是涉及政治,百分之40的内容是涉及体育,对于这种不确定性,只是简单的将新闻聚类到某一簇中是不太合适的。
另外,可以发现K-means自带的属性就是簇的形状是圆形的,即使可以对坐标进行加权处理,产生的也都是和坐标轴对齐的椭圆。

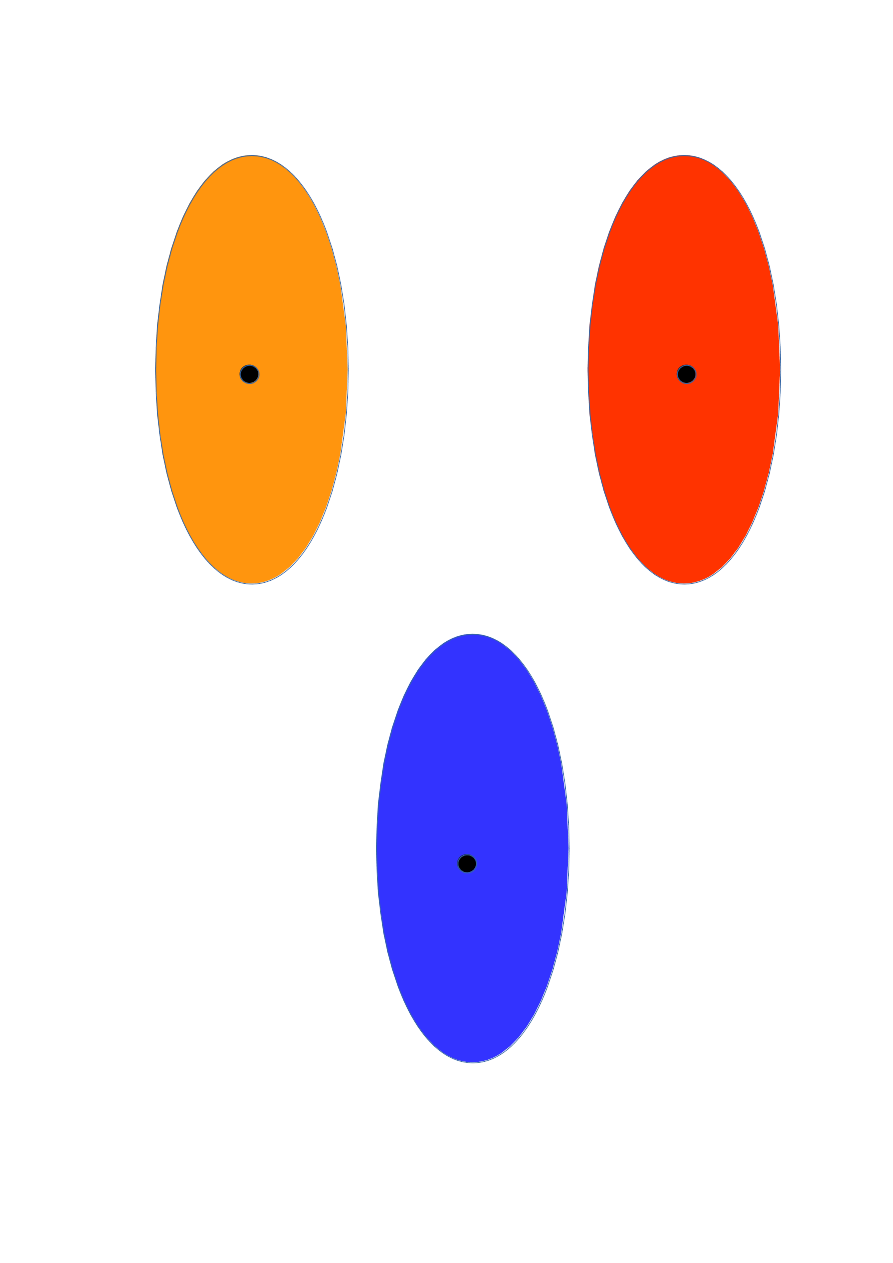
但是我们可以看一些K-means失效的情况。比如下面几个例子:
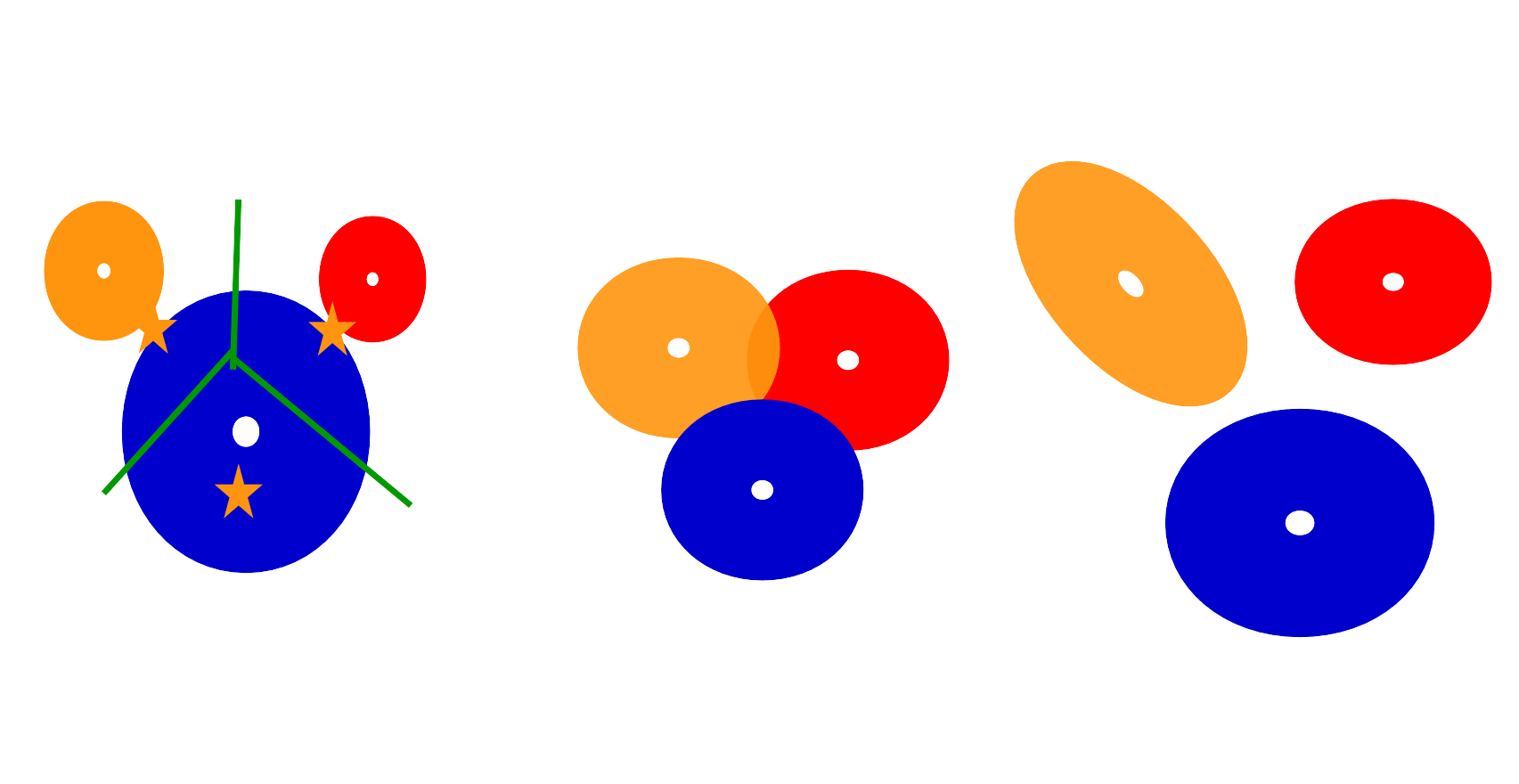
第一个例子,由于簇的大小不一样,导致簇中心的偏移;第二个例子,簇中样本的重叠这种情况k-means无法处理;第三个例子,簇的方向并为与坐标轴对齐,这种k-means也无法处理。
所以,基于混合概率模型的聚类方法应运而生。这种方法有以下优点:
- 使用的是
soft assignment处理簇分配不确定性的情况 - 不仅能发现簇的中心,还能学习到簇的形状
- 能够学习到决定簇时不同维度特征的权重(例如计算文章簇分配时,学习到每个单词的权重)
下面讲讲用的比较多的高斯混合聚类。
高斯混合聚类
假设服从多元高斯分布,则其概率密度函数为:
在此我们记为:
定义高斯混合分布为:
假设样本是由高斯混合分布产生的,其中为样本选择第个混合成分的概率。
那么在给定样本的情况下,选择哪个高斯分布呢?
为方便,记。
对于给定一个数据集,通常是利用极大似然估计模型参数。
对数似然:
EM算法求解
前面,我们提到过通常用EM算法进行参数隐变量的估计,在这里,是隐变量。分为两步E步,M步。 E步:利用当前模型参数计算,进而求的期望,在这里就是上面我们求的; M步:利用求得的$LL(D){ (\alpha _i,\mu _i,\Sigma _i) | 1\leq i \leq k }$$。
要使最大化,我们对模型参数分别求导,令导数为0即可。
最终可求得:
对于求解,还需要满足
我们可以采用拉格朗日乘子法求解。构造:
可求得:
上面是GMM学推导,其结果是非常符合我们的直觉的。观察就可以发现,其实GMM的参数也就是普通高斯模型的加权而已。
上面是关于EM算法的一轮推导,那么EM算法如何对GMM进行初始化呢?
EM算法估计GMM参数的初始化
有很多种方法可以初始化EM算法,但是选择合适的初始化显得至关重要,这对算法的收敛速率和寻找到的局部最优解的质量很重要。
GMM的整个求解过程图例
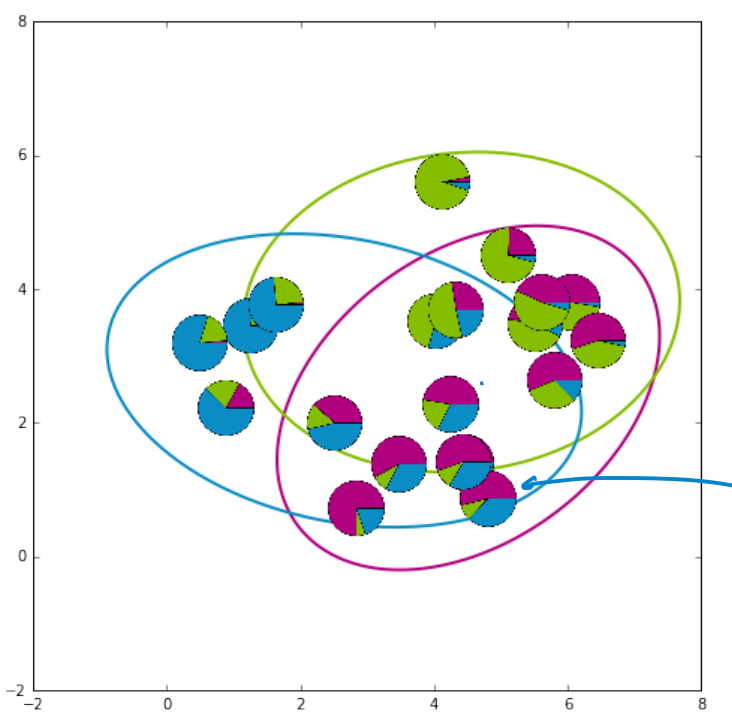
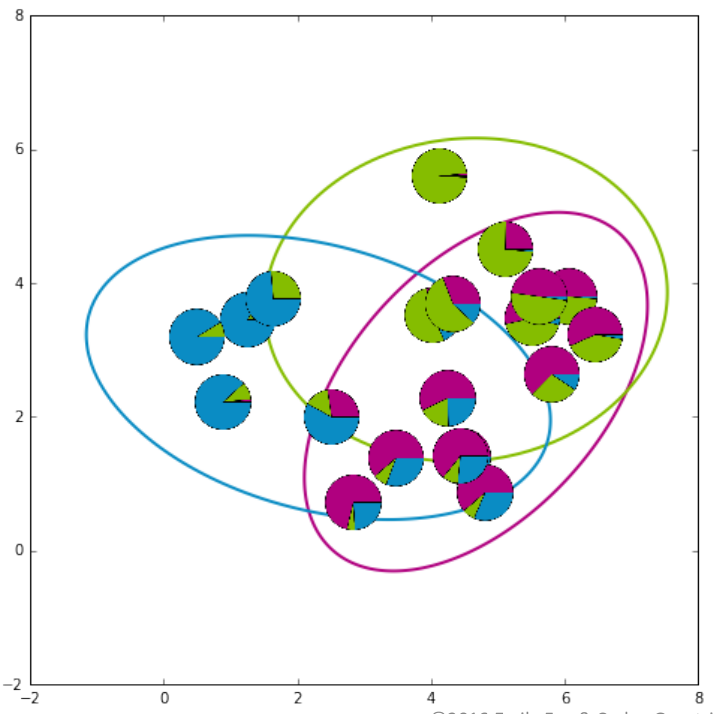
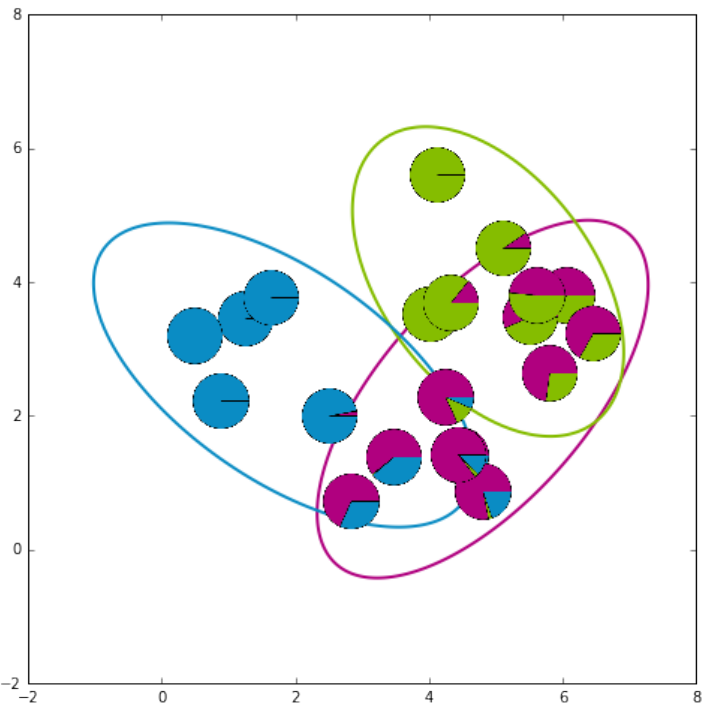
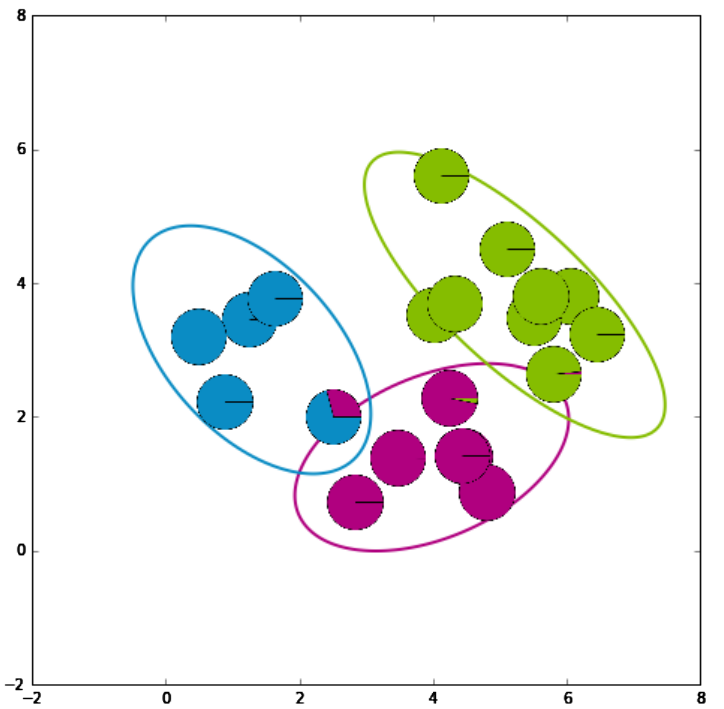
从上到下,从左到右,
- 第一张图:初始化;
- 第二张、第三张图:迭代E,M计算,消除非重合处的不确定性;
- 第四张图:收敛,可以看到最后只有在簇重合处才会有不确定性。
过拟合
大家可能会好奇,在这个模型中,什么情况下会出现过拟合呢?
当似然概率无限大的时候!!!!
有没有觉得很不可思议,怎么可能出现无限大的情况,且看看来说个子丑寅卯。在概率密度函数中,分母可是出现了项的,当这一项(也就是方差)为0的时候,OK,无穷大便产生了。这是数学意义上的,那么在数据集中样本的分布则对应着什么情况呢?
比如,K=2,只有两个簇的时候,其中一个簇只有一个样本属于它,剩余的都属于另外一个簇。这个时候,对于只有一个样本的簇,它的方差为0!!!!
通常在数据的维度很高时,数据分布很稀疏,很容易以出现这种情况。比如,对于对文章聚类时,每个词语都是文章的一个维度时,假如某个词只有一篇文章有或者所有的文章拥有这个词的数目一致时,此词的出现的次数的分布的方差为0。
即:<=>最大化
参考文献
[1] 机器学习,周克华