通常谈分类模型之类的评价指标谈得很多,在此我们以二分类为例。
模型的评价
讲真,对于模型的评价中的各个指标,不知为何,我总是容易弄混淆。因此这里我也分享下将这些指标区分清楚的一些小tricks。
首先定义一下分类混淆矩阵,这是推导后面所有概念的基础。
| 实际\预测 | Positive | Negative |
|---|---|---|
| Positive | TP | FN |
| Negative | FP | TN |
- TP:正例被预测为正例的数目
- FN:正例被预测为负例的数目
- FP:负例被预测为正例的数目
- TN:负例被预测为负例的数目
接下来,正式介绍用的比较多的几个评价指标。
Accuracy
准确率,这个是比较容易理解的。就是分类正确的样本的数目占样本总数的比例。
其中,是分类函数,是指示函数,取值1或者0。
Recall and Precision
通常在web搜索或者信息检索中,我们想搜索我们需要的信息,那么如何评价信息系统的性能呢?它展示的信息是否都是我想要的呢?我想要的信息有多大部分被展示了呢? 这两个概念可能稍微难以理解一点,不过如果翻译的中文意思形象点非常有助于我们的理解。在这里,我将Recall翻译为“查全率”,也就是“我想要的信息有多大部分被展示了呢”;Precision翻译为“查准率”,指的是“展示的信息里有多大部分是我想要的”。我觉得配上这个背景去理解这两个概念,基本上没什么问题了。下面来看看它们的数学定义:
可以看出,Recall和Precision是一对有矛盾的量。要想Recall达到1,我们只需要展示所有的信息就好了,但是这个时候Precision可能就会很低;反之,要想Precision很高,我们只展示我们最有把握的信息就好了,但这个时候,可能还有很多我们感兴趣的信息没有被展示出来,这样Recall可能就会变低。
根据不同的Recall和Precision的值,我们可以作出一个以Precision为横坐标,Recall为纵坐标的P-R曲线。对于两条不相交的曲线,显然,外围的曲线更优。
通常,为了综合考虑这两个指标,我们会用F1 Score这一综合考虑两者的指标来评价学习器的好坏。F1 Score越大学习器性能越好。
Recall for Fixed K
但在是实际应用中,假设我们只展示K个结果,这个时候我们应该关注对于固定的K的时候的效果如何。也许对于所有的结果而言Recall不太好,但是对于一个固定的K每次都是我们想要的结果就很好了。
ROC and AUC
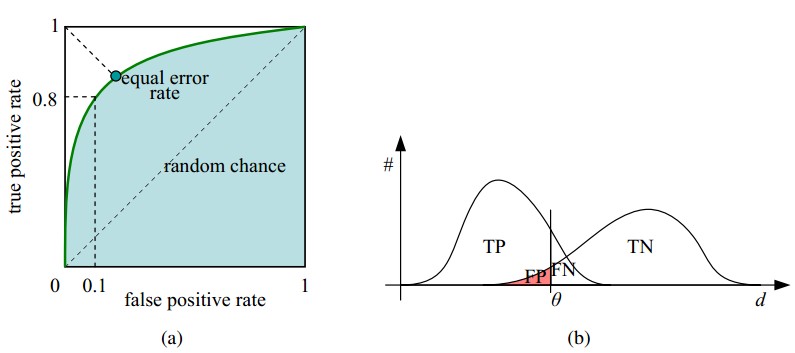
下面来讲讲ROC曲线和AUC。ROC曲线的横坐标是“真阳性率”TPR(True Positive Rate),纵坐标是“假阳性率”FPR(False Positive Rate)。这两个名字应该也都是可以望文生义的。 TPR是正样本里预测为正例的比率;FPR是负样本里预测为正例的比率。
AUC(Area Under ROC Curve)求的就是ROC曲线下的面积。
如下图,通过设置不同的分类阈值,随着分类阈值的减小,越来越多的样本被预测为正例。因此,从这一点来看,AUC是很看重样本预测的排序质量的。假设样本的排序质量用排序损失函数来衡量。那么
其中,、分别是正例和负例的数目;是指示函数;并且假设对数据集中的每一对正例、负例对,若正例预测值小于负例,则惩罚1,若正例预测值等于负例,则惩罚0.5。
同样,对于两条不相交的曲线,外围曲线的学习器性能更佳。